Gravity
As Refraction
Ned Phipps
Copyright © 2009
Extract:
This paper analyzes refraction from overlapping idealized
refractive mediums. Describing
refraction in terms of a metric and using a 
energy potential for
the mediums gets an effect that exactly matches the measured PPN gravity parameters
and 
. The metric allows
for an exact solution for the case of a central mass. Finally a neutron star collapse is discussed.
Introduction:
Refraction is not a complex effect, especially when considering idealized contexts. My own thought process for gravity as refraction is to start with ordinary refraction through glass. I notice that light through an idealized glass is Lorentz invariant within the glass, but with a different speed of light. Because local Lorentz invariance is usually a feature only for gravity and curved space, it becomes possible to start imagining the features of GR being fully possible without a generalized metric. I take the transparent glass and morph it into a gravity theory.
I will present, first, the equations, and then elaborate each one. They are ordered in a natural way so as to start with ordinary refraction and move toward the specific gravity refraction.
The bottom line is that this theory passes the PPN tests.
The Set of Equations
Refraction can be described by the following metric:
The speed-of-light is necessarily related to an energy potential:
Overlapping effects are multiplied:
With a distributed mass density this takes the form:
Using the natural default potential of 
the combined metric is
simply:
This metric exactly matches the PPN parameters and as measured by solar
system tests2. The metric
predicts the next PPN parameters.
This metric allows for an exact solution for the orbit around a central mass.
The radius of collapse for a neutron star is:
Elaborations
Equation 1:
Refraction is often described as an effect associated with the speed of light being slower in a medium such as glass. It is usual to say that the wavelength is shortened because of the speed change and that the frequency remains the same. This is described by the metric equation:
We more often see the equation written this way:
and it is the same because, for light, 
.
It is actually, however, mathematically not required that only the wavelength changes. It is just as valid to have the effect shared between distance and time effects. This theory assumes a flat Minkowski space-time where gravity is a refractive process within that space-time. Using light through glass as a model, the metric would be isotropic and diagonal and have the following form:
Simple metric theory tells us that:
and the first two equations satisfy this.
Mathematical symmetry would suggest the following metric:
This has the property
Perhaps this can be derived from theory about refraction of massive particles. The equation satisfies properties of light successfully and that has traditionally been the more difficult side of gravity theories. Here, the difficulty has switched to gravity of massive particles. Later I will outline the field theory process of refraction that indicates how massive particles can also be refracted.
Qualitatively, I interpret the metric to mean that objects
are, natively, smaller by the factor 
, and they, natively, move in slow motion by the factor 
.
Equation 2:
Gravity is being described as refraction through an idealized medium. As such, there is no exchange of particles as in the other forces. This is similar to refraction of light, where the photon is considered the particle that is being affected, but the affectation is via the fields interfering rather than a new interaction. With refraction of light, the photon is created outside the glass. As it goes through the glass it is the same photon (field interaction) and exits the glass still as the same photon and finally reaches another charged particle and is absorbed. With gravity it is the same. Without an exchange of particles, the energy of the affected masses remains the same. How? Well, as follows:
Starting with the total energy equation:
Let’s start at rest at elevation 1:
Let the mass freefall to elevation 2 where we define:
First, if a mass is moved to a different elevation, it has a
different mass according to the metric. The mass is reduced by the factor. The difference is
made up as kinetic energy 
. We describe the difference
via the potential difference
.
So,
Defining this with 
at infinity and 
as the mass at infinity gives us our main equation.
Note: The statement “the mass is reduced” is a core element of this theory. It implies that gravity affects particles in a way that causes them to have a different “effective” mass – that there is a gravitational process involved that naturally changes this “effective” mass.
Equation 3:
Gravity is being described as refraction. Let’s idealize the
glass so that it is a perfect space, 
described by its index
of refraction 
. Now, let’s put another glass sphere, 
, within this context. has an index of
refraction 
. Without elaboration, we can see that the combine index of
refraction is 
. The speed of light is reduced by the factor from the already
reduced speed as defined by :
or, more generally for N overlapping mediums,
This is the same as if is put within , or if we just say that the two mediums have merged. This is
also the result if we consider the mediums to be probability fields. The
combined effect is multiplied, not summed.
Equation 4:
In the following we describe an object with mass as having a simple mass distribution and that the size of the distribution is small enough to ignore. We are attempting to analyze the difference between using a product of effects and using a sum of potentials.
Let a mass M be divided into N equal parts, each producing
an effect with potential 
. The combined effect is the product of these:
We can find the limit of this as we divide it into more and more parts. Multiplying out equation gives:
Each term within the sums is equal, so we need to just count how many terms we have. That comes from the choose function and gives:
or, since we will be taking the limit, we can keep only the high order terms in each item:
or
So we get our main equation:
Individual particles are not point masses, so each particle would start with the effect given by this equation.
Merging the effects of multiple particles results in adding the exponents and we can use a composite potential, again, that adds individual contributions.
Equation 5:
This is a straight substitution into equation 1.
PPN comparison with experimental observation
and GR
Parameterized Post-Newtonian Gravity:
The PPN has many terms
dealing with dynamics and different forms of energy and their possibly
different gravitational effects. Here we
will ignore all of them and simply use the terms associated with regular
matter.
The PPN reduces to a
diagonal matrix with:
where .
For this paper, we
will expand it slightly so that space and time both have the same order terms.
The expansion, I
believed, is defined, by convention, so that GR values are 1.
For GR we get the
approximation from the Schwarzschild metric:
Changing the radial
coordinate makes the metric isotropic1 and ready for a direct PPN
approximation.
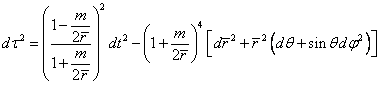
where
We can now fill out
the values for the coefficients using Taylor series expansions. For GR we get (by default):
Isotropic Schwarzschild Metric (GR):
|
|
|
|
|
|
|
|
Refraction Metric:
The new metric is much simpler.
Phipps Refraction Metric:
|
|
|
|
|
|
|
|
Solving the geodesic equations for a central
mass3
The following will
take the metric through an analysis of the central mass planetary orbits in a
manner that directly parallels the derivation that is done for GR. The process
is to calculate the geodesic equations and solve them for acceleration in r. The geodesic equations are:
(implied summation)
where
(implied summation)
are the Christoffel
symbols. For the metric in this paper,
we only have the diagonal elements. So
the Christoffel symbols reduce to
(no implied summation)
The metric, in
spherical coordinates is:
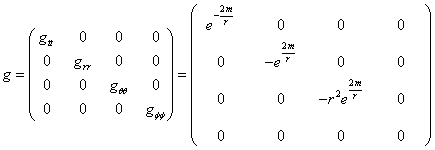
To calculate the
Christoffel symbols, we will need all the partial of the metric. These are all zero except for the following
partial in r:
The Christoffel symbol
are:
(note: 
for a diagonal metric)
This gives the
Geodesic equations as:
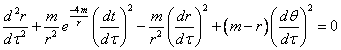
Integrating the first
and third equations results in:
Where 
and 
are constants of
integration.
We can now use these
in the original metric. Substituting 
and 
back into the original
metric and dividing by 
gives:
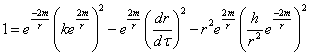
or, simplifying:
Solving for 
gives:
Taking the derivative of this with respect to 
:
Canceling the 
and finally solving for 
, we get
The equations , , and together represent an EXACT SOLUTION for the problem of motion about a central
mass.
Neutron Star Collapse
With GR, the neutron
star collapse results in a singularity.
This has traditionally been considered a catastrophic problem. The
metric of this theory includes the collapse of a neutron star, but without a
catastrophic singularity. Consider the following simple thought experiment:
An object is at a
distance 
from a central
mass. That central mass will be the
combined mass of a collapsing neutron star.
As an object descends toward 
, the object gets smaller in each of its 
dimensions according
to 
. How many of these
objects can be fit in a circle (perimeter) around the center?
The “normal” ratio,
without any gravitational distortion, gives
As 
, you can’t fit any objects in a circle around the
center. With gravity included, we get
This number is at a
minimum when its derivative is zero.
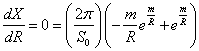
So the minimum happens at
It is at this point
that particles shrink faster than the collapse and the star can no longer
maintain its structure. It’s at this
radius where any additional collapse effectively causes more relative space
between particles and I call this the inversion point. This is the point after which, from a local
point of view, the universe begins to expand.
Field
Theory of Refraction
I make this
assumption: Glass is transparent to individual photons. Let’s look at the process of one photon being
emitted, travel through glass, and get absorbed and recorded on the other side. Field theory defines this as calculation of
the probability of the final absorption.
The calculation is an integral over all possible paths from emission to
absorption.
The photon takes all
possible paths through the glass. Some of the paths include one or more
scatterings. Each scattering results in a 90-degree phase shift. When the paths
are merged, the random scatterings cancel each other out and the effect is
equivalent to a slower velocity.
The controlling
interaction is a single scattering of a photon by a glass molecule. It is the
nature and consistency of this scattering that makes the glass transparent. It
is just this scattering event that I am morphing into a gravity theory. So,
here’s a Feynman diagram of the interaction.4
Figure 1
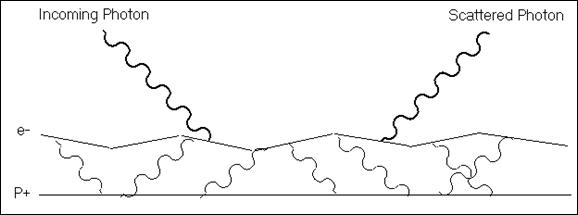
This shows the heavy nucleus
as stationary, an electron interacting with the nucleus, and the photon being
absorbed and reemitted. The absorbing electron is a non-localized electron.
The complex glass
molecule can be described as a pseudo-particle. The interaction becomes an s-channel
interaction and looks like this:
Figure 2
Finally, we simply
relabel the particles.
Figure 3
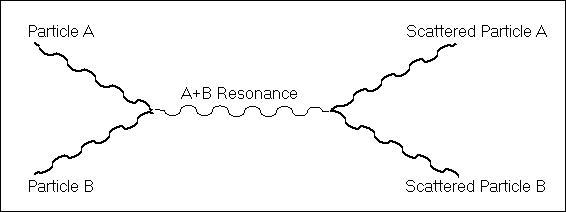
We have two masses
that merge momentarily into a resonance state that then decays back to the original
particles but in random directions – a standard scattering event. This last diagram encompasses the entirety of
this theory of gravity. The “medium“
referred to throughout this paper is simply the particles, themselves, as they
interact non-locally in standard field-theory processes. The density of such
interactions would naturally decrease by distance at a 
rate. The effect would be refraction. The interaction, being
entirely non-local, would naturally be very small.
Furthermore, this
effect is eerily similar to the simpler travel through the vacuum. The creation of multiple paths for
“integrating all paths” could be this same phenomenon where particles are
continuously scattered by a homogeneous background.
Intriguing
Cosmic Model
GR describes a neutron
star’s collapse to a singularity. The
following is a very intriguing alternative:
As a neutron star gets
smaller, the gravity metric effect is also making the particles smaller.
At m/r = 1.0, the gravity
metric effect is faster than the radius reduction. Viewed from inside the
neutron star, the star is now expanding and the external collapse cannot be
stopped.
The metric effect rips
the star apart.
Since the star is a
neutron star, this implies an unimaginably large fission reaction.
The energy from this
fission reaction produces an enormous number of new particles pairs (matter and
anti-matter) all in the context of a high gravity metric.
As the gravity effect
continues to make the particles smaller and less massive, conservation of
energy enables an even more enormous number of new particles.
A great deal of the
fission reaction energy escapes to the exterior universe. The rest, remaining in the interior, becomes
part of a new apparently expanding universe.
The matter and
anti-matter quickly segregate themselves into an interior of one kind and a
halo around the interior of the other kind.
The gravity in the interior continues to function as in the exterior, with the gravity between nearby particles dominating the effects. As the process continues, the particles group themselves into galaxies and stars and so on.
The original neutron star had much matter that did not immediately fall into the interior. A good deal of this external matter will recollapse through the inversion point and race inwards.
The gravity effect of this matter will affect the interior and make it appear to expand even faster.
Since this second wave flew through the inversion point more easily, it might eventually catch up to the original interior. Perhaps it catches up almost immediately.
If the original neutron star has a companion whose orbit falls into the collapsing star, then that matter will affect the interior’s apparent expansion. Perhaps that matter could result in our observed accelerating expansion.
References:
1: “Gravitation”, Misner, Thorne and Wheeler, 1973
2: “Lunar Laser Ranging Tests of the Equivalence Principle with the Earth and the Moon”, James G. Williams, Slava G. Turyshev, Dale H. Boggs, 2004
3: “Anomalous Precessions”, http://www.mathpages.com/rr/s6-02/6-02.htm
4: “QED: The Strange Theory of Light and Matter”, Richard P. Feynman, 1985
5: “Gravity, A Rigorous Derivation of the Gravitational Field” (anonymous) 1987