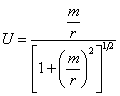A Heretical Theory of Gravity - Adjusted
Ned Phipps
Copyright © 2006
Introduction:
A 1987 anonymous paper developed a time and space distortion
associated with gravity using accepted principles of physics. This was done, in
a static context, assuming the existence of an energy potential difference
between elevations. Searching for a time
and space distortion along similar lines to Special Relativity gave the
essential result of:
![]()
![]()
where ![]() represents an energy
potential. Using the standard energy
potential from Newton
represents an energy
potential. Using the standard energy
potential from Newton
completes the theory1.
I couldn’t find
anything wrong with the analysis. As
such, I felt compelled to research General Relativity and look more closely at
the paper. I continued to find no problems with the paper’s analysis, but I
found that the comparisons with GR were very wrong (understatement here). This paper makes a PPN comparison with GR to
distinguish the two theories. The new
one does not match the recent measurement of ![]() . (At the time it was written, there was no such
measurement.) Only one place seemed
available to make an adjustment. The
resulting modified metric eliminates the event horizon and has a perfect limit
at
. (At the time it was written, there was no such
measurement.) Only one place seemed
available to make an adjustment. The
resulting modified metric eliminates the event horizon and has a perfect limit
at ![]() . There is also a
prediction for the next PPN parameter
. There is also a
prediction for the next PPN parameter ![]() . This theory has an additional advantage in that it presumes
that the universe is fundamentally flat, a recently concluded fact from CBR
analysis.
. This theory has an additional advantage in that it presumes
that the universe is fundamentally flat, a recently concluded fact from CBR
analysis.
Converting to a
metric model:
His analysis
represents a distortion of space and time that is embedded in a flat
spacetime. This is inconsistent with GR
in the general sense. However, it is
absolutely comparable to the Schwarzschild metric and also to the PPN
approximation. The Schwarzschild metric is an exact solution of
GR for the case of a spherically symmetric central mass and the spacetime
around that mass. It and the PPN remain
the main means of analyzing gravity affects in the solar system.
The following is mostly
in spherical coordinates ![]() with
with ![]() for the orbital
precession analysis.
for the orbital
precession analysis.
The proposed scale
factors can be put into a standard metric form. Starting with the flat metric:
![]()
and using the scale
factors as ![]() and
and ![]() applied to the above
gives:
applied to the above
gives:
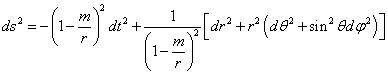
The Schwarzschild
metric, in its original form, has the simplest look:
![]()
This would tend to
indicate that GR is fundamentally anisotropic where mass causes distortions in
the time and radial directions with a plus/minus symmetry.
The PPN
approximation of GR and the gravity of this paper:
Underlying the PPN is
a flat space and an isotropic gravitational effect. The gravity of this paper takes those as fundamental properties
rather than as a part of an approximation technique. This paper only considers the static metric, but we should be
able to build the full dynamic metric with only the PPN technique. Simply fill out the off-diagonal elements in
the standard PPN way. As such, other
features, such as gravity waves, should result from this theory.
The PPN has many terms
dealing with dynamics and different forms of energy and their possibly
different gravitational effects. Here
we will ignore all of them and simply use the terms associated with regular
matter.
The PPN reduces to:
![]()
![]()
where ![]() is the same as eq. .
is the same as eq. .
For this paper, we
will expand it slightly so that space and time both have the same order terms.
![]()
![]()
The expansion, I
believed, is defined, by convention, so that GR values are 1.
![]()
![]()
![]()
For GR we get the
approximation from the Schwarzschild metric:
![]()
Changing the radial
coordinate makes the metric isotropic2 and ready for a direct PPN
approximation.
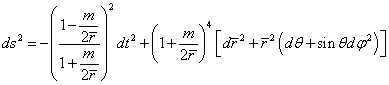
where
We can now fill out
the values for the coefficients using Taylor series expansions. For GR we get (by default):
![]()
![]()
![]()
For the gravity of this paper (so far):
![]()
![]()
![]()
Radar and laser
delay are used to measure the PPN coefficients ![]() ,
,![]() :
:
NASA now has tens of
thousands of ranging data points. These
started with planetary radar ranging an 1967 and now include extra high
precision laser ranging to planetary probes.
At the time of the initial publishing of the base theory in this paper, ![]() was measured
to be 1.0 and there was no measurement of
was measured
to be 1.0 and there was no measurement of ![]() . In other words, it was as accurate as GR. The latest measurements are from lunar laser ranging. These
have nailed
. In other words, it was as accurate as GR. The latest measurements are from lunar laser ranging. These
have nailed ![]() at 1.0 to 4 decimal
places3. Future gravity measurements are expected to
be able to measure
at 1.0 to 4 decimal
places3. Future gravity measurements are expected to
be able to measure ![]() .
.
A modification is possible:
Considering the basic
premise of the theory in this paper, the only place for modification appears to
be in the formula for U. It is assumed
that gravity is essentially a ![]() force with a
force with a ![]() energy function. Let’s discover the difference between this
theory (as it currently stands) and the measured values. Consider this modified form:
energy function. Let’s discover the difference between this
theory (as it currently stands) and the measured values. Consider this modified form:
Let’s try modifying
the potential so that it reads:
![]()
where
![]()
where
![]()
What we have is an
effective distance for the potential that is affected by the context of the
gravity potential itself. Basically,
gravity happens in the context of gravity.
This is quite reasonable.
![]()
Assuming the
measurements of the PPN parameters, we can get a long ways toward discovering
an ![]() that matches the
data.
that matches the
data.
We have
![]()
We already know ![]() ,
, ![]() , and
, and ![]() . Also,
. Also, ![]() and
and ![]() .
.
Now,
![]()
or
![]()
Also,
![]()
so
![]()
or
At ![]()
![]()
so
![]()
We find ![]() as follows. Starting with eq.,
as follows. Starting with eq.,
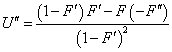
and
![]()
Also, from eq.,
![]()
So
![]()
or
![]()
We have:
![]()
or
![]()
Here, this author
makes a guess at a full function for F.
Let
![]()
This would be
consistent with ![]() ,
,![]() , and
, and ![]() . We can now find a
modified energy function
. We can now find a
modified energy function ![]() .
.
![]()
or
![]()
or
or
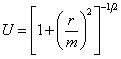
The metric needs to be
restated.
![]()
where
![]()
and
![]()
is the “effective”
radius for calculating the energy function.
Speculation on ![]() :
:
This is a space
“dilation” or “expansion” formula. Can
something be considered to be moving with velocity ![]() ? With special
relativity, the distance the traveler travels “constracts”. This is equivalent to the traveler, himself,
expanding. It seems difficult to apply
such an interpretation.
? With special
relativity, the distance the traveler travels “constracts”. This is equivalent to the traveler, himself,
expanding. It seems difficult to apply
such an interpretation.
Without a geometric
meaning for the radius, I believe that gravity cannot be a direct effect. To me it seems to be an effect that defines
the springiness of space that is required for Quantum Field Theory to work.
The Lorentz Transforms
can be either an Aether derivation or a Relativity derivation. If the gravity effect is an adjustment of
the springiness of a fixed Aether, then the speed-of-light adjustments slow
light with respect to the speed of the Aether and this doesn’t work.
If the spacetime is
fundamentally a flat Minkowski space with 4 dimensions, we get the natural
inclination to use x(t), y(t), z(t) because there is only one of the
opposite-type dimensions. Starting with
this kind of space and the existence of springiness for Quantum Physics,
gravity can be an effect that changes this springiness.
If spacetime is not
fundamentally Minkowski, then the background Aether could possibly be a gravity
Aether from our universe’s mass and/or external mass. The ![]() formula could be a reflection of how gravity effects add
together when dynamics are considered.
formula could be a reflection of how gravity effects add
together when dynamics are considered.
One nice effect of
this “effective” radius is that ![]() is now well
behaved. As
is now well
behaved. As ![]() ,
, ![]() , not infinity. Furthermore, this is nicely monotonic and
, not infinity. Furthermore, this is nicely monotonic and ![]() is well behaved as
well:
is well behaved as
well:
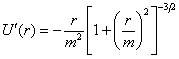
and
![]()
With no gradient of ![]() at the center of any
mass, however large the mass happens to be, there is no force there – no
singularity – no traditional black hole.
at the center of any
mass, however large the mass happens to be, there is no force there – no
singularity – no traditional black hole.
This nice effect may
be the real indicator of what the adjustment means. If the space and time distortions are the result of some
mechanism or gravity process, then they must always be finite.
Clear prediction:
This metric predicts a
new PPN value for ![]() from the second
derivative of the space metric. Here we
have to change our labeling. The PPN
has
from the second
derivative of the space metric. Here we
have to change our labeling. The PPN
has ![]() by definition. So we will use the letter
by definition. So we will use the letter ![]() .
.
![]()
![]()
![]()
Starting with eq. rewritten here as:
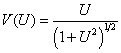
So
![]()
![]()
Reading off ![]() and
and![]() , we finally have from eq.
, we finally have from eq.
![]()
The predicted value
for ![]() is one third of this (double check via the GR metric):
is one third of this (double check via the GR metric):
![]()
Dynamics:
Although the gravity
of this paper is developed from a static model, we can make it fully
dynamic. One way is to defer to the
PPN. Another is more constructive. We can simply give gravity a speed. The gravity potential becomes simply the
time-delayed potential based on that speed.
There are two natural speeds that can be considered. One is the speed of light based on the
metric itself. The other is to have the
speed-of-gravity be the faster speed of light that would occur without
gravity. All these variations feel
internally consistent.
Breaking the Rules:
Imagine, instead of a
metric definition, the following: First
consider a glass sphere with an index of refraction. Light bends toward the center of the sphere as it enters. The standard way of calculating the bending
of light is to consider light as a wave with a wavefront that is perpendicular
to the direction of travel. The process
of tracking the bending of light is identical to tracking a geodesic. The tracking works for any entity described
as a wave with a wavefront. If there is
a side-to-side gradient in the index of refraction then the light - or any
particle described as a wave - curves.
Replace the glass sphere with an aether that, as you get closer to the
central mass, has a stronger index of refraction. With this approach, the
classic aether, instead of being dragged around by the masses, is actually
created by the masses. How? Perhaps it is zero-mass, zero-spin,
zero-energy, infinite speed gravitons emitted from every mass - an infinite
number of them forming a graviton density in a fixed 3D space. Perhaps it affects the springiness of space
that allows quantum mechanics to work.
In any case, an aether formulation needs to be considered again in a
rigorous way. Note: a “light clock”
embedded in glass will run slower and be the same size. The metric for light inside glass would have
g00=1/n, gii=1. If the effective substance
of the glass “aether” was made from stuff that is much smaller than an atom,
then the change in the speed of light would affect the size of the atoms
embedded in it. In other words, the
size of the light clock would shrink.
We would get a metric at least very similar to the one in this paper.
Cosmic Models and
Collapse:
All three theories
include the collapse of a neutron star. With GR, the neutron star collapse results in a singularity. This has traditionally been considered a
catastrophic problem. In the original heretical theory, when 0.5 < U < 1,
objects moving toward the center from an external frame-of-reference appear to
be moving away from each other in their local frames-of-reference. He argues that our universe could be a
collapsing neutron star. The following
highlights that the modified theory also has this inversion. Consider the following:
An object is at a
distance R from a central mass. That
central mass could be the combined mass of a collapsing neutron star. As an object descends toward R=0, the object
gets smaller in each of its x,y,z dimension according to S = S0*(1-U). How many of these objects can be fit in a
circle around the center. The “normal”
ratio, without any gravitational distortion, gives
As ![]() , you can’t fit any
objects in a circle around the center.
With gravity included, we get
, you can’t fit any
objects in a circle around the center.
With gravity included, we get
![]()
For ![]() ,
,
![]()
So we get the
asymptotic ratio
Comparing with we see a clear inversion. The inversion point appears to be where when
![]() is just a little
larger than
is just a little
larger than ![]() .
.
References:
1) “Gravity, A
Rigorous Derivation of the Gravitational Field” (anonymous), 1987
2) “Gravitation”,
Misner Thorne and Wheeler, 1973
3) Lunar Laser Ranging
Tests of the Equivalence Principle with the Earth and the Moon, James G.
Williams, Slava G. Turyshev, Dale H. Boggs, 2004