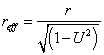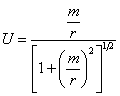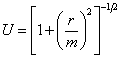Home

Gravity Made Simple

Ned Phipps

Statement of the Theory:

First, define the following metric:

Define, also, a scalar gravitational energy potential and set

Define as the time-delayed Newtonian potential with a modified “effective” radius. Time-delayed means the radial distance is calculated according to the speed of gravity. This speed is either the speed of light (as defined here) or 1. There is currently no “speed-of-gravity” measurement to decide this experimentally.

where is the “effective” radial distance to each mass.

Let

Properties:

1) Low-gravity: Compares well with the isotropic form of the Schwarzschild metric. When expanded as a Taylor’s series in , ,,, all match. This means that the theory passes all the solar system tests including the recent measurement of the PPN parameter .

2) Medium-gravity:

a. This theory predicts the next PPN parameter to be twice that of GR.

3) High-gravity:

a. The event horizon of a black hole is reduced to a single point at the center.

b. The collapse approaches, but never reaches the singularity.

c. The metric effect outpaces the actual collapse at around 1.272*m/r.

d. The appearance from within the collapse is comparable to the external universe. It appears to be expanding.

4) General: One coordinate system covers the entire universe.

Interpretation:

The intuitive interpretation of this theory is that all particles are refracted by a gravitational aether. The mathematics of geodesic paths and refraction paths are equivalent. The difference is only that the underlying space is not considered curved when interpreting paths as refraction.

The “effective” distance is a kind of equilibrium condition where gravity happens in the context of gravity. The same combined applies to all masses and the final value is not known to each mass. The calculation for the gravity from a single mass is relatively simple. For multiple masses, one iterates from a guess. The iterative concept is a strong clue for the process that would be required to accomplish the effect.

Single Central Mass:

For the case that matches the Schwarzschild context, equations and can be solved for the energy potential and, hence, the metric. The energy potential is the following:

This highlights the well-behaved nature of the potential at and .

References:

1) “Gravity, A Rigorous Derivation of the Gravitational Field” (anonymous), 1987

2) “ A Heretical Theory of Gravity – Adjusted” Ned Phipps, 2006