Spheres and Lattices
A Word About Purpose
The sphere is probably the most commonly encountered shape in nature. Whether we are talking about celestial bodies, about liquid droplets, about human cells - the “natural” tendency is for them to acquire some kind of spherical shape (or at least a close approximation of it). Furthermore, physical bodies in general tend to “cluster together” so that they take the least amount of volume. It is from such observations that the natural question came about : what is the most efficient way of “packing” a certain number of balls such that they will use up “most” of the space in which they reside?
If we were to deal with cubes, the answer would be trivial - given any volume, it can be filled up to 100% with different sized cubes (by a process resembling volume integration). Spheres, however, do not behave as nicely - there will always be space left in between them. Although it may sound relatively simple, the answer to the general question “what is the highest density of spheres that can be attained?” is one of the famous open problems in mathematics. The answers currently known only address particular cases of the problem in which the arrangement of the spheres follows certain rules.
Besides being fascinating mathematical problems, it turns out that sphere packings and lattices actually do have a lot of theoretical as well as practical applications. Here are just a few[1]:
“The best packings turn out to have connections, sometimes totally unexpected with other branches of mathematics. [..] In 24 dimensions, the Leech lattice l24 has mysterious connections with hyperbolic geometry. There are direct applications of lattice packings to number theory, for example in solving Diophantine equations and to the “the geometry of numbers.”
There are important practical and theoretical applications of sphere packings to problems arising in digital communications. Just to give the flavor, here is a typical question from the design of spread-spectrum communications for mobile radio : how many spheres of radius 0.25 can be packed into a sphere of radius 1 in 100 dimensional space ?”
Two and three dimensional packings have many applications. For example, the circle in a two dimensional packing may represent optical fibers as seen in the cross-section of a cable.”
Format
This article is divided into two parts. The first part will deal with computing a formula for the volume of spheres in Ân. This computation will yield the rather disturbing conclusion that as n increases, the sphere of radius 1 will fill less and less of the cube of side 2 in which it can be naturally inscribed. As n approaches infinity, the ratio of the volume of the sphere to the volume of the circumscribed cube becomes 0.
The second part of the article will tie in the previous result with the big picture by investigating some of the results already known in the theory of sphere packings and lattices.
The Volume of Balls in  n
In an abstract sense, a ball is defined by means of providing a center R and a radius e. The ball Be (B of radius e) is then defined as the set of all points within distance e of R :
Be = { c Î Ân : d(c, R) £ e },
whered is the natural (Euclidean) metric on Ân.
For n=1 the ball is just a segment of “volume” (length) 2*r; for n=2, the ball is a circle (with “volume” = p * r2); for n=3, the ball is a sphere (with the well known volume = 4 * p * r3 / 3 ). What about higher dimensions ? The answer is quite far from obvious. Here’s a derivation using Cavalieri’s principle :
Intuition :
The crux of the proof relies on noticing the relationship between the volume of balls in Ânand in Ân-1. Take for example, a circle (ball in Â2), centered at the origin, with some arbitrary radius r. If we “slice” the circle with vertical lines, perpendicular to the X axis, each and every such slice is in fact a “ball” of a certain radius in Â1. Here’s a visual representation of this fact :
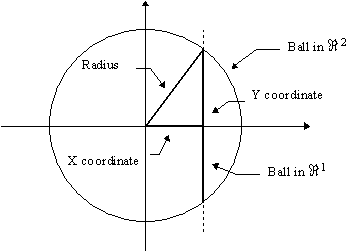
The vertical slice generates a “ball” in Â1 (because of symmetry
considerents : obviously, the center of the ball would be the point
of intersection of the slice with the X axis and the radius would
be ![]() , where r is the radius of the
ball in Â2). To compute the volume of
the ball in Â2, we use Cavalieri’s
principle :
, where r is the radius of the
ball in Â2). To compute the volume of
the ball in Â2, we use Cavalieri’s
principle :
![]() , where by V1 we mean
“the volume of the ball in Â1 “ (see above). The volume of the ball in Â2 is generated by
“moving” the vertical slice along the X axis, from the
point (-r, 0) to the point (r, 0). The formula for V2
(x) could be expressed as
, where by V1 we mean
“the volume of the ball in Â1 “ (see above). The volume of the ball in Â2 is generated by
“moving” the vertical slice along the X axis, from the
point (-r, 0) to the point (r, 0). The formula for V2
(x) could be expressed as
![]()
The problem is, at this point, that the evaluation of the above integral is very difficult. In order to resolve this difficulty, we will attempt to establish a relationship between the volume of balls in Â3and the volume of balls in Â1, and then use change of variable. Again, here is the intuitive step :

This time, we start off with a sphere (ball in Â3) and make the first slice perpendicular to the X axis. The cross section is a circle (ball in Â2). Furthermore, we slice the circle with a vertical line (as in the previous derivation) and, once again, obtain that the cross section is a ball in Â1. This all amounts to the following formula for the volume of the sphere in Â3 in terms of V1 (volume of ball in Â1):
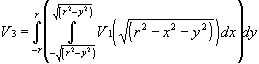
Intuitively, we note that the above integral basically means that we move span the volume of the 3 dimensional sphere by means of “moving” the 2 dimensional slice along the X axis. In turn, the volume of the 2 dimensional ball is generated by “moving” the 1 dimensional slice along the “axis” local to the 2 dimensional ball. The rest follows from 2 trivial applications of the Pythagorean theorem. At this point, we apply the change of variable formula (from rectangular to polar coordinates)
![]()
and we get the following, easy to compute integral :
![]()
At this point, we can compute a few of these volumes. We know that V1 (x) = 2*x and V2 (x) = Pi*x2. By repeatedly applying the formula above, we get
![]() ;
;![]()
![]() ;
;![]()
![]() ;
; ![]() ; etc...
; etc...
By induction, the two following remarkable results can be derived :
![]() and
and ![]()
Notice now, that given the volume of the natural circumscribed cube (of side length 2, “centered” at the origin), the ratios of the volume of the sphere to the cube become, as n approaches infinity become (the volume of the cube of side 2 in n dimensions is
V = 2n) :
![]() and
and ![]() .
In other words, as pointed at the beginning of the article, the
sphere fills less and less of the volume of the cube inside which
it lies, as the dimensions become larger and larger. Ultimately,
the sphere fills “nothing” inside its circumscribed
cube (!)
.
In other words, as pointed at the beginning of the article, the
sphere fills less and less of the volume of the cube inside which
it lies, as the dimensions become larger and larger. Ultimately,
the sphere fills “nothing” inside its circumscribed
cube (!)
Lattices and Sphere Packings
As pointed out in the introduction to this article, spheres cannot fill a given volume as well as cubes can. In fact, on average, spheres can only fill approximately 75% of any given enclosed space (here, by spheres we mean 3D balls). The “natural” way in which balls would arrange themselves if dropped inside a box would be something like this :
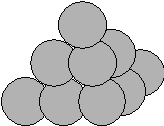
This arrangement, which is encountered very
often in nature (think for example of a stack of cannon balls), is
known as the “face-centered cubic (or fcc)
lattice.” In this packing, it has been shown that the
spheres occupy ![]() of the
total space. The sphere density would then be the volume of the
enclosure times 0.7405 divided by the number of balls. The question
arising is then “is this the greatest density that can be
attained?”. Unfortunately, this problem is unsolved. For
years, a result proven by Rogers stated that no sphere packing can
have density greater than .7796 (in 3D), but recently this result
has been tightened to .7784 by Lindsey. It is widely believed, but
still left to be proven, that the actual upper bound is 0.7405 (in
other words, the density obtained above)[2].
of the
total space. The sphere density would then be the volume of the
enclosure times 0.7405 divided by the number of balls. The question
arising is then “is this the greatest density that can be
attained?”. Unfortunately, this problem is unsolved. For
years, a result proven by Rogers stated that no sphere packing can
have density greater than .7796 (in 3D), but recently this result
has been tightened to .7784 by Lindsey. It is widely believed, but
still left to be proven, that the actual upper bound is 0.7405 (in
other words, the density obtained above)[2].
Lattices :
Simply put, a “lattice packing” has the property that 0
(i.e. the Origin) is a center and, given u, v centers of spheres,
then both (u+v) and (u-v) are centers of spheres in the lattice.
This property somewhat resembles the definition and properties of a
basis for a vector space : in Â3, we can find 3
centers, v1, v2 and v3 (or
n such centers for Ân) such that the set of
all centers of spheres in the lattice are linear combinations of
those centers (i.e. given any center Cr, it can be
expressed as ![]() , where ki are real
numbers[3].
, where ki are real
numbers[3].
With this new bit of information, we can now define the generator matrix for the transformation
 , where vij are the
components for the basis vectors.
, where vij are the
components for the basis vectors.
The Gram Matrix for the lattice is
defined as ![]() .
.
With this notation, the definition for the density of a lattice packing becomes :
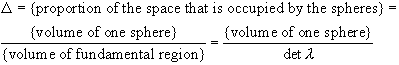
By fundamental region, we mean the
parallelotope consisting of the points ![]() .
.
Let’s take a look at an example (this particular one is also very famous and is called the hexagonal lattice. This particular arrangement of spheres resembles the geometry of a beehive):
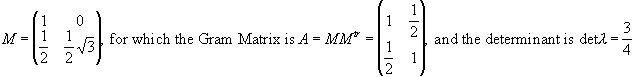 .
.
The fundamental region is then simply
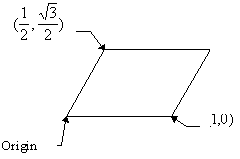
The lattice looks somewhat like this :
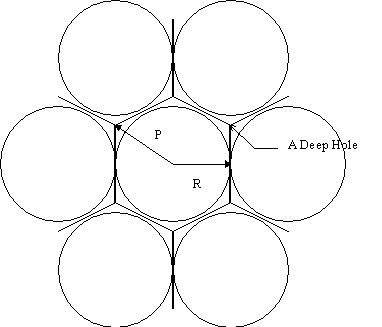
Notice the hexagon surrounding each sphere in the packing (which is what suggests the name of the packing). The vertices of the hexagons are called “Deep Holes”, being equall far from the centers of the spheres surrouding them.
The above sphere packing has been shown to have the highest density in 2 dimensions (the density is 0.9069). Similarly, in 3 dimensions, the fcc lattice described at the beginning of this unit has the highest density (result proven by Gauss).
As the dimension of the space increases, the density decreases (for
example, in 4 dimensions, the density D4=0.6169, while
in 24 dimensions, the density is ![]() ).[4] Just to give you an idea of
the dynamics of the densities, here is a table :
).[4] Just to give you an idea of
the dynamics of the densities, here is a table :
|
Name |
Density |
|
l0 |
1 |
|
l1 |
1 |
|
l2 |
0.90690 |
|
l3 |
0.74048 |
|
l4 |
0.61685 |
|
l5 |
0.46526 |
|
l6 |
0.37295 |
|
l7 |
0.29530 |
|
l8 |
0.25367 |
|
l12 |
0.04173 |
|
l24 |
0.001930 |
Bibliography:
1. C.H. Edwards - Advanced Calculus of Several Variables
Academic Press New York and London
2. J.H. Conway and N.J.A. Sloane - Sphere Packings, Lattics and Groups
Springer-Verlag