The Theory of Special Relativity

Albert Einstein, working in the Swiss Patent Office, published the paper On the Electrodynamics of Moving Bodies in the German journal Annalen der Physik in 1905, his third paper to be published that year. In this paper, Einstein outlined the major ideas of the special theory of relativity, the theory that opened physics from a dead science where it was beginning to look like everything had already been discovered to a new world of possibilities. It finally laid to rest the idea of ether, the massless invisible medium through which light was thought to propagate. More importantly, it showed physicists that the world does not necessarily operate ways that are intuitive. It made physics a little more abstract, and more difficult to visualize, at least at very high speeds...
The theory of relativity says that all laws of physics are the same in all inertial frames of reference. An inertial frame of reference is a frame of reference which is moving at a constant velocity relative to an observer. The observer's frame of reference is generally considered to be "at rest", although this does not mean the same thing as Newton's absolute rest. A person making an observation about something else that is in motion can consider himself at rest relative to the object he is observing. This is true in any case where the object is moving at a constant velocity, that is, not accelerating with respect to the observer. If any two people observed each other as they moved in different directions, each person could consider himself at rest, and the other person moving. Both points of view are equally valid, according to special relativity.
Another postulate of the special theory of relativity is that light has a constant velocity c, which is the same regardless of the velocity of the object which emits the light. It is also the same speed for any observer in any inertial reference frame. This is not very intuitive, since it would seem that the light emitted from a flashlight moving at a speed of, say, 0.5c relative to an observer would have a velocity of 1.5c relative to the observer. According to relativity, however, the observer will measure the velocity of the light coming from the moving flashlight at c.
We can boil down special relativity into its two basic principles:
- All laws of physics are the same in all inertial reference frames. - This means for example that if you were to observe a large asteroid moving past you, you can consider yourself to be at rest relative to the asteroid. But if you were on the asteroid, you could consider yourself at rest and the Earth moving past. If you were to perform experiments on the Earth and on the asteroid, the results would be the same. You could not devise an experiment to test whether you are in motion or the asteroid were in motion. (You could almost say that the universe really does revolve around you...but there's more on that in general relativity.)
- The speed of light is constant and is the same to all observers, regardless of their reference frame. - At least as long at it is a reference frame at a constant velocity. Special relativity is restricted to reference frames that are at a constant velocity, not accelerating or rotating.
Since the speed of light is the same for all observers, there is a problem of reconciling the case when two people, one moving relative to the other, turns on a flashlight in the direction of his movement. If the second person were moving at a speed of v relative to the observer, then the light coming out of his flashlight, according to Newton, would be moving at a speed of c + v relative to the observer. However, because of the second postulate above, the observer will measure the speed of light coming from the flashlight as c. How can this happen? The answer goes back partly to Fitzgerald and Lorentz. According to these two, objects in motion contract in length in the direction of their movement. Now we can't really say that the beam of light contracts in length, but we can say that the distance travelled by the beam of light contracts. To illustrate this, we will need a better explanation of a frame of reference, or how we measure distances.
Try to imagine a three dimensional axis, with x, y, and z axes. Now let's assume that this set of axes is a frame of reference, at rest relative to an observer. Any object at rest relative to the origin of this set of axes (the distance from the origin to the object remains constant) can be considered to be in this frame of reference. An object in motion relative to the origin of our first set of axes can be considered to be in another frame of reference, at motion relative to our frame of reference. (By the way, we can really only call it "our" frame of reference when we are at rest relative to one another, otherwise we would be in our own separate reference frames.)
Now a point in your reference frame will coincide with a point in my reference frame. We'll call your reference frame S and the point in your reference frame (x, y, z, t), t for time, we'll my reference frame S' and the point in my reference frame (x', y', z', t'). Now, if my reference frame is moving at a velocity v in the direction of the x axis, then after a time t, my reference frame will be displaced from yours a distance of vt. According to the Galilean transformation, your point P(x, y, z, t) will be the point P'(x-vt, y, z, t) in my frame of reference. This makes sense in any normal case. But it turns out there are problems with this conclusion.
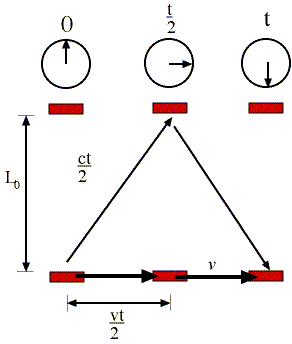
Lets say we constructed a clock that kept time by bouncing a beam of light back and forth between two mirrors. Every time the light wave hit the bottom mirror, the clock would tick off one second. To anyone where the clock were at rest, this would seem perfectly normal. However, if the clock were in motion relative to you, you would notice something strange. As the clock moved by, it would appear to tick more slowly than a clock at rest relative to you. This comes from the fact that light has a constant speed in all inertial reference frames. We can demonstrate why the clock ticks more slowly like this: we have our clock of two mirrors, with the mirrors a distance of L apart. If the clock moves perpendicular to its length (see figure) then light bouncing between the mirrors will actually be moving a distance greater than L. If the clock moves a distance vt, the light will have to travel a distance of 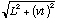 to get to the second mirror. Since the speed of light is constant at c, it will take it a time
to get to the second mirror. Since the speed of light is constant at c, it will take it a time 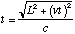 seconds to make the trip. However, if I observe the clock in the its reference frame, I will see that same light wave make its trip in a time
seconds to make the trip. However, if I observe the clock in the its reference frame, I will see that same light wave make its trip in a time 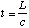 since it is at rest and the speed of light is also c in this reference frame. Since the time is greater to you, who is watching the clock move by, than to me, who is watching the clock at rest, it turns out that time slows down for objects in motion relative to the observer. According to the equations given by Fitzgerald and Lorentz, and later Einstein, time slows by a factor of
since it is at rest and the speed of light is also c in this reference frame. Since the time is greater to you, who is watching the clock move by, than to me, who is watching the clock at rest, it turns out that time slows down for objects in motion relative to the observer. According to the equations given by Fitzgerald and Lorentz, and later Einstein, time slows by a factor of 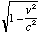 , so to calculate the time measured by someone moving by at a speed of v, you use the formula
, so to calculate the time measured by someone moving by at a speed of v, you use the formula 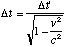 , where x is the distance travelled. You can remember this by remembering the saying moving clocks run slow.
, where x is the distance travelled. You can remember this by remembering the saying moving clocks run slow.
Time dilation is not the only consequence of the constancy of the speed of light. Let's say that we wanted to a trip to a star that is 15 light years away. This distance is known as the proper length, the length measured from a reference frame where the distance or object measured is at rest. If we were to make the trip a 0.75 times the speed of light, then it should take 20 years, right? Well if you made the trip and I stayed at home, it would appear to me that 20 years had passed. But to you, because of time dilation, time will go by more slowly for you than for me. In 20 years for me, more than 20 years will have passed for you. According to the formula above, 30.2 years will have passed for you. That means you will have arrived at the star 10.2 years ago. To find out how long it took you to get to the star in my time frame (since the 20 years is obviously too long) we can use the length contraction formula derived by Lorentz and Fitzgerald, ![L=L[0]*sqrt(1-(v^2)/(c^2)) ALIGN=top>, where <IMG SRC=](images/lfformula.gif) is the proper length. Using this formula, the distance you travelled will not be 15 lightyears, but 9.9 lightyears. At 0.75c, it will take you 13.2 years to make the trip. So after 13 years, you will have travelled the 15 lightyears to the star, but to you, it was only a 10 lightyear trip.
is the proper length. Using this formula, the distance you travelled will not be 15 lightyears, but 9.9 lightyears. At 0.75c, it will take you 13.2 years to make the trip. So after 13 years, you will have travelled the 15 lightyears to the star, but to you, it was only a 10 lightyear trip.
Poincaré had proposed before that the speed of light was an impassible speed limit in the universe. Einstein thought that a way for this to happen was for mass to increase as size increased. Newton's force equation F=ma states that the force needed to accelerate and object is proportional to its mass. So, as you accelerate to speeds approaching the speed of light, there is more mass, and hence more force is needed to accelerate more. Since applying a force on an object to move it increases its kinetic energy, the more force you apply, the more energy it has. The energy of the object will increase as the force increases, and the force will increase as the mass increases, until, well, you run out of energy to continue accelerating the object. According to Einstein, there isn't enough energy in the universe to accelerate a single grain of sand to the speed of light, since its mass would increase to infinity. The formula for mass increase is ![m=m[0]/(sqrt(1-<v^2)/(c^2))](images/massinc.gif) . This can be derived in the following way. Suppose we have two balls of mass
. This can be derived in the following way. Suppose we have two balls of mass ![m[0]](images/mnaught.gif) which collide perfectly elasticly. One ball is in the S frame, and one is an another frame, S', which is moving at a velocity v, in the positive x direction relative to S. The two balls are thrown at each other with a velocity V, such that V=V', where
which collide perfectly elasticly. One ball is in the S frame, and one is an another frame, S', which is moving at a velocity v, in the positive x direction relative to S. The two balls are thrown at each other with a velocity V, such that V=V', where ![V[a]](images/va.gif) is the velocity of the S ball in the y direction, and
is the velocity of the S ball in the y direction, and ![V[b]'](images/vbprime.gif) is the velocity of the S' ball in the -y direction. If the balls originally started a distance L apart, then the time it will take the ball in S to strike the S' ball and rebound to its original position will be
is the velocity of the S' ball in the -y direction. If the balls originally started a distance L apart, then the time it will take the ball in S to strike the S' ball and rebound to its original position will be ![T[0]=L/V[a]](images/traveltime.gif) as measured in frame S. In S', the ball will make the trip in the same time,
as measured in frame S. In S', the ball will make the trip in the same time, ![T[0]=L/V[b]](images/traveltime2.gif) . Linear momentum must be conserved in the S frame (in the S' frame
as well, but here we'll conventrate of the S frame), so it must be true that
. Linear momentum must be conserved in the S frame (in the S' frame
as well, but here we'll conventrate of the S frame), so it must be true that ![m[a]v[a]=m[b]v[b]](images/nmom.gif) . In the S frame,
. In the S frame, ![V[b]](images/vb.gif) is found to be
is found to be 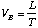 where T is the time for the S' ball to make its round trip as seen in S. In S', the trip will take the time
where T is the time for the S' ball to make its round trip as seen in S. In S', the trip will take the time ![T[0]](images/tnaught.gif) , where
, where ![T=T[0]/sqrt(1-(v^2/c^2))](images/timechange.gif) . If we replace T with this equation in the formula for
. If we replace T with this equation in the formula for ![V[b]](images/vb.gif) , we get
, we get ![V[b]=L*sqrt(1-(v^2/c^2))/T[0]](images/vbexp.gif) . Since we also know from
. Since we also know from ![T[0]=L/V[a]](images/traveltime.gif) that
that ![V[a]=L/T[0]](images/vatime.gif) . When we substitute these values for
. When we substitute these values for ![V[a]](images/va.gif) and
and ![V[b]](images/vb.gif) into the linear momentum formula, we get
into the linear momentum formula, we get =m[b](L*sqrt(1-(v^2/c^2))/T[0])](images/linmomfilled.gif) . This simplifies to
. This simplifies to ![m[a]=m[b]*sqrt(1-(v^2/c^2)](images/linmomsimple.gif) . Since
. Since ![m[a]](images/ma.gif) =
=![m[b]](images/mb.gif) =
=![m[0]](images/mnaught.gif) when measured in the same frame of reference(i.e. they are at rest relative to one another), then in the S frame, we can sat the S ball has a mass
when measured in the same frame of reference(i.e. they are at rest relative to one another), then in the S frame, we can sat the S ball has a mass ![m[0]](images/mnaught.gif) and the S' ball, which is moving with a speed v relative to S and the S ball, has a mass m, and the formula above follows from this.
and the S' ball, which is moving with a speed v relative to S and the S ball, has a mass m, and the formula above follows from this.
The relativity of mass leads to the relativity of momentum, which classically is given by p=mv. We can simply use the formula above for mass, and we get the relativistic formula for momentum, ![p=m[0]v/(1-(v^2/c^2))](images/relmom.gif) . We can also figure out what relativistic force is going to be. Classically, force is equal to the mass of an object times its acceleration, where acceleration is the change in velocity with respect to time,
. We can also figure out what relativistic force is going to be. Classically, force is equal to the mass of an object times its acceleration, where acceleration is the change in velocity with respect to time, 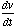 . But relativistically, both mass and velocity will vary with time. If we look at the equation for force as
. But relativistically, both mass and velocity will vary with time. If we look at the equation for force as 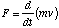 , this takes into account the non-constant mass. Using the chain rule for derivatives, we get
, this takes into account the non-constant mass. Using the chain rule for derivatives, we get 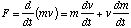 .
.
Einstein's most famous equation found from the postulates of special relativity is 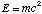 . In this formula, E is the total energy of a particle of mass m. Now, since mass increases with velocity, it follows that energy increases with velocity. A particle at rest has a certain mass, and this mass is known as its rest mass,
. In this formula, E is the total energy of a particle of mass m. Now, since mass increases with velocity, it follows that energy increases with velocity. A particle at rest has a certain mass, and this mass is known as its rest mass, ![m[0]](images/mnaught.gif) . A particle in motion will have a certain kinetic energy, KE, which is given by the classical formula
. A particle in motion will have a certain kinetic energy, KE, which is given by the classical formula 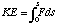 . Using the formula for force from above, we can re-write the KE equation as
. Using the formula for force from above, we can re-write the KE equation as 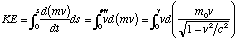 . If we integrate the last term by parts(
. If we integrate the last term by parts(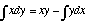 ),
), 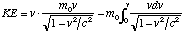 . Working our way down, we end up with
. Working our way down, we end up with
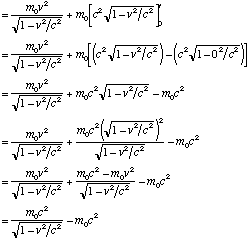
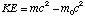
This result shows that the kinetic energy of an object is equal to the increase its mass due to relative motion (![m-m[0]](images/massdiff.gif) ) times the speed of light squared. We can re-write the equation for kinetic energy as
) times the speed of light squared. We can re-write the equation for kinetic energy as 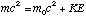 .
. 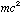 is interpreted as the total energy of the object, E. When it is at rest (KE=0), it still has energy,
is interpreted as the total energy of the object, E. When it is at rest (KE=0), it still has energy, 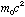 . This energy is called the rest energy. The total energy of an object with kinetic energy is
. This energy is called the rest energy. The total energy of an object with kinetic energy is 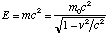 .
.
It is this equivalence of mass and energy that becomes apparent in nuclear reactions, where a small amount of matter can produce large amounts of energy. It also explains the amounts of energy emanating from stars, as fusion reactions release huge amounts of energy.
All of these effects are derived from two simple postulates, that light is the same speed to all observers, and that the same laws of physics apply to all inertial reference frames. These postulates, however, are only valid in inertial reference frames. In reference frames that are accelerated, or which are subject to a gravitational field, the theory of general relativity must be used.
Back to the index!
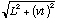 to get to the second mirror. Since the speed of light is constant at c, it will take it a time
to get to the second mirror. Since the speed of light is constant at c, it will take it a time 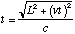 seconds to make the trip. However, if I observe the clock in the its reference frame, I will see that same light wave make its trip in a time
seconds to make the trip. However, if I observe the clock in the its reference frame, I will see that same light wave make its trip in a time 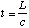 since it is at rest and the speed of light is also c in this reference frame. Since the time is greater to you, who is watching the clock move by, than to me, who is watching the clock at rest, it turns out that time slows down for objects in motion relative to the observer. According to the equations given by Fitzgerald and Lorentz, and later Einstein, time slows by a factor of
since it is at rest and the speed of light is also c in this reference frame. Since the time is greater to you, who is watching the clock move by, than to me, who is watching the clock at rest, it turns out that time slows down for objects in motion relative to the observer. According to the equations given by Fitzgerald and Lorentz, and later Einstein, time slows by a factor of 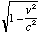 , so to calculate the time measured by someone moving by at a speed of v, you use the formula
, so to calculate the time measured by someone moving by at a speed of v, you use the formula 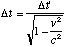 , where x is the distance travelled. You can remember this by remembering the saying moving clocks run slow.
, where x is the distance travelled. You can remember this by remembering the saying moving clocks run slow. 

![L=L[0]*sqrt(1-(v^2)/(c^2)) ALIGN=top>, where <IMG SRC=](images/lfformula.gif) is the proper length. Using this formula, the distance you travelled will not be 15 lightyears, but 9.9 lightyears. At 0.75c, it will take you 13.2 years to make the trip. So after 13 years, you will have travelled the 15 lightyears to the star, but to you, it was only a 10 lightyear trip.
is the proper length. Using this formula, the distance you travelled will not be 15 lightyears, but 9.9 lightyears. At 0.75c, it will take you 13.2 years to make the trip. So after 13 years, you will have travelled the 15 lightyears to the star, but to you, it was only a 10 lightyear trip.![m=m[0]/(sqrt(1-<v^2)/(c^2))](images/massinc.gif) . This can be derived in the following way. Suppose we have two balls of mass
. This can be derived in the following way. Suppose we have two balls of mass ![m[0]](images/mnaught.gif) which collide perfectly elasticly. One ball is in the S frame, and one is an another frame, S', which is moving at a velocity v, in the positive x direction relative to S. The two balls are thrown at each other with a velocity V, such that V=V', where
which collide perfectly elasticly. One ball is in the S frame, and one is an another frame, S', which is moving at a velocity v, in the positive x direction relative to S. The two balls are thrown at each other with a velocity V, such that V=V', where ![V[a]](images/va.gif) is the velocity of the S ball in the y direction, and
is the velocity of the S ball in the y direction, and ![V[b]'](images/vbprime.gif) is the velocity of the S' ball in the -y direction. If the balls originally started a distance L apart, then the time it will take the ball in S to strike the S' ball and rebound to its original position will be
is the velocity of the S' ball in the -y direction. If the balls originally started a distance L apart, then the time it will take the ball in S to strike the S' ball and rebound to its original position will be ![T[0]=L/V[a]](images/traveltime.gif) as measured in frame S. In S', the ball will make the trip in the same time,
as measured in frame S. In S', the ball will make the trip in the same time, ![T[0]=L/V[b]](images/traveltime2.gif) . Linear momentum must be conserved in the S frame (in the S' frame
as well, but here we'll conventrate of the S frame), so it must be true that
. Linear momentum must be conserved in the S frame (in the S' frame
as well, but here we'll conventrate of the S frame), so it must be true that ![m[a]v[a]=m[b]v[b]](images/nmom.gif) . In the S frame,
. In the S frame, ![V[b]](images/vb.gif) is found to be
is found to be 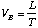 where T is the time for the S' ball to make its round trip as seen in S. In S', the trip will take the time
where T is the time for the S' ball to make its round trip as seen in S. In S', the trip will take the time ![T[0]](images/tnaught.gif) , where
, where ![T=T[0]/sqrt(1-(v^2/c^2))](images/timechange.gif) . If we replace T with this equation in the formula for
. If we replace T with this equation in the formula for ![V[b]=L*sqrt(1-(v^2/c^2))/T[0]](images/vbexp.gif) . Since we also know from
. Since we also know from ![V[a]=L/T[0]](images/vatime.gif) . When we substitute these values for
. When we substitute these values for =m[b](L*sqrt(1-(v^2/c^2))/T[0])](images/linmomfilled.gif) . This simplifies to
. This simplifies to ![m[a]=m[b]*sqrt(1-(v^2/c^2)](images/linmomsimple.gif) . Since
. Since ![m[a]](images/ma.gif) =
=![m[b]](images/mb.gif) =
=![p=m[0]v/(1-(v^2/c^2))](images/relmom.gif) . We can also figure out what relativistic force is going to be. Classically, force is equal to the mass of an object times its acceleration, where acceleration is the change in velocity with respect to time,
. We can also figure out what relativistic force is going to be. Classically, force is equal to the mass of an object times its acceleration, where acceleration is the change in velocity with respect to time, 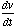 . But relativistically, both mass and velocity will vary with time. If we look at the equation for force as
. But relativistically, both mass and velocity will vary with time. If we look at the equation for force as 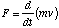 , this takes into account the non-constant mass. Using the chain rule for derivatives, we get
, this takes into account the non-constant mass. Using the chain rule for derivatives, we get 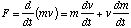 .
. 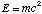 . In this formula, E is the total energy of a particle of mass m. Now, since mass increases with velocity, it follows that energy increases with velocity. A particle at rest has a certain mass, and this mass is known as its rest mass,
. In this formula, E is the total energy of a particle of mass m. Now, since mass increases with velocity, it follows that energy increases with velocity. A particle at rest has a certain mass, and this mass is known as its rest mass, 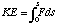 . Using the formula for force from above, we can re-write the KE equation as
. Using the formula for force from above, we can re-write the KE equation as 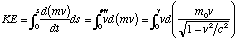 . If we integrate the last term by parts(
. If we integrate the last term by parts(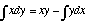 ),
), 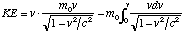 . Working our way down, we end up with
. Working our way down, we end up with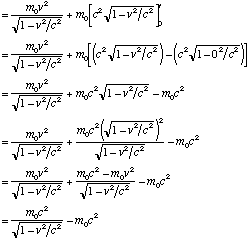
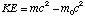
![m-m[0]](images/massdiff.gif) ) times the speed of light squared. We can re-write the equation for kinetic energy as
) times the speed of light squared. We can re-write the equation for kinetic energy as 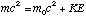 .
. 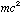 is interpreted as the total energy of the object, E. When it is at rest (KE=0), it still has energy,
is interpreted as the total energy of the object, E. When it is at rest (KE=0), it still has energy, 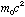 . This energy is called the rest energy. The total energy of an object with kinetic energy is
. This energy is called the rest energy. The total energy of an object with kinetic energy is 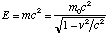 .
.